
Implied oddsy nie są wprawdzie trudne do zrozumienia, ale wielu pokerzystów korzysta z nich podczas gry w niewłaściwy sposób. Prowadzi to do wielu kosztownych błędów. Aby ich uniknąć, zapoznajcie się z przygotowanym przez Upswing Poker poradnikiem poświęconym właśnie konceptowi implied oddsów.
Czym są implied oddsy?
Implied oddsy to ilość pieniędzy, jakie spodziewasz się zarobić na późniejszych ulicach, jeśli trafisz jeden ze swoich outów. Koncept ten, wraz z pot oddsami, jest powszechnie używany do zrozumienia, czy możemy opłacalnie sprawdzić beta przeciwnika, trzymając rękę drawującą.
Jeśli spodziewasz się, że po trafieniu swojego drawa zarobisz dodatkowe pieniądze, wówczas posiadasz dobre implied oddsy. Jeśli przewidujesz jednak, że na przyszłych ulicach nie będziesz w stanie uzyskać żadnych dodatkowych pieniędzy, twoje implied oddsy są słabe albo wręcz zerowe.
Precyzyjne obliczenie implied oddsów jest niemal niemożliwe, ponieważ wymagałoby rozważenia niezliczonej ilości zmiennych – każdej możliwej karty, akcji, sizingu itd., które mogłyby pojawić się na przyszłych ulicach. Z tego powodu możemy jedynie pokusić się o pewne logiczne szacunki.
Co w takim razie możemy obliczyć z większą dokładnością? Ano minimalną kwotę, jaką musiałbyś wygrać na przyszłych ulicach, aby usprawiedliwić nieopłacalne w innych okolicznościach sprawdzenie. Właśnie tym zajmiemy się poniżej.

Jak działają implied oddsy?
Wyobraź sobie, że uczestniczysz w cashówce na stawkach 1$/2$. Trzymasz KQ i grasz na turnie z pozycją. Board przyniósł A629 – posiadasz zatem drawa do nutsowego koloru – a twój przeciwnik betuje za 15$ do puli wynoszącej 20$.
Szybkie obliczenie pot oddsów (15$ do sprawdzenia / [15$ bet + 20$ pula + 15$ call] = 0,3) pokazuje, że aby zagrać dochodowego calla, musisz posiadać equity wynoszące ponad 30%. Jako że na turnie posiadasz tylko około 20-procentową szansę na trafienie flusha, musiałbyś spasować swoją rękę, jeśli nie wziąłbyś pod uwagę ostatniej ulicy.
W tym momencie do akcji wkraczają implied oddsy. Oto wzór na obliczenie, jak wiele pieniędzy musiałbyś wygrać na riverze, aby usprawiedliwić sprawdzenie na turnie:
15$ (kwota do sprawdzenia) / 15$ (bet przeciwnika) + 20$ (rozmiar puli) + 15$ (kwota do sprawdzenia) + X$ (jaką kwotę będziesz musiał wygrać na riverze) = 0,2 (equity twojej ręki)
Jak widać, wzór na implied oddsy nie różni się znacząco od wzoru na pot oddsy. Jedynymi różnicami są dodane „X” w mianowniku i equity twojej ręki po prawej stronie równania.
Rozwiążmy zatem niewiadomą z powyższego wzoru.
15$/ (15$ + 20$ + 15$ + X$) = 0,2
15$ / (50$ + X$) = 0,2
0,2 * 50 + 0,2 * X = 15$
0,2 * X = 5$
X = 25$
Oznacza to, że aby call na turnie był dochodowy, musisz wygrać ponad 25$, gdy trafisz na riverze kolor z KQ. Jako że pula już w tym momencie wynosi 50$, przeciwnik musiałby na ostatniej ulicy zagrać beta za połowę puli.
Wydaje się to jak najbardziej możliwe do zrealizowania. A trzeba jeszcze pamiętać, że potencjalnie możemy wygrać dużą pulę, np. w sytuacji, kiedy rywal również trafi kolor. Dlatego w przypadku tego rozdania sprawdzenie na turnie jest poprawnym zagraniem.
Przykłady implied oddsów
Big blind vs button (pula z jednym raisem, gramy jako preflop caller)
Przypuśćmy, że sprawdziłeś na big blindzie z J7 i grasz bez pozycji. Sprawdziłeś także c-bet rywala na flopie. Na turnie – board: KT32 – przeciwnik z buttona zagrywa beta za 50$ do puli 67$. W stacku pozostało mu 117$ – ty dysponujesz większym stackiem.
Twoje pot oddsy wynoszą: 50$ / 167$ = 30% – to equity, które potrzebujesz do dochodowego sprawdzenia.
Oto, jak wygląda twoje equity (oznaczone fioletowym kwadratem) w starciu z dobrze zrównoważonym zakresem double barreli:
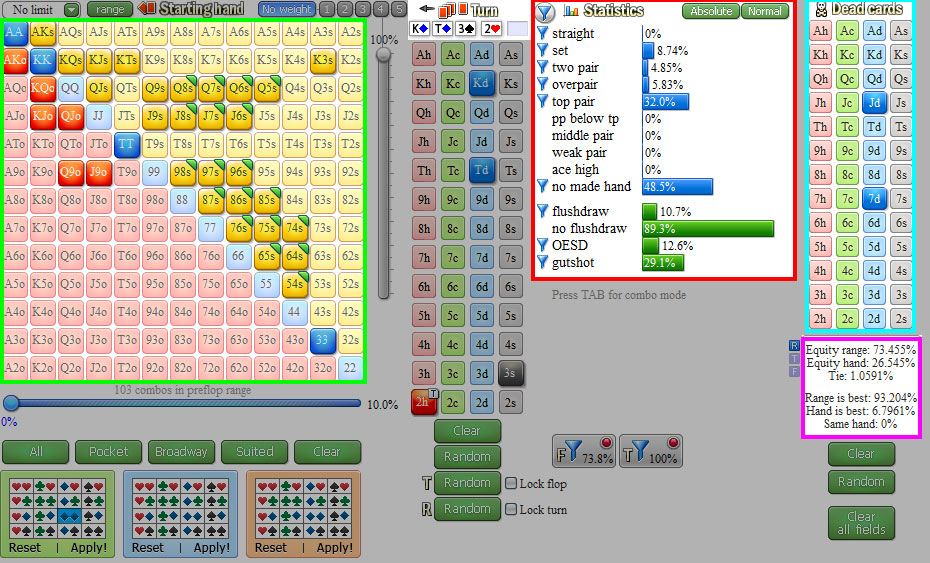
Można zauważyć, że posiadamy 26,5-procentowe equity – dlatego jeśli weźmiemy pod uwagę wyłącznie pot oddsy, equity jest niewystarczające. To jednak niekompletna ocena sytuacji – nie wzięliśmy wszak pod uwagę tego, co może wydarzyć się na riverze.
Trafimy kolor na riverze w 19,6% przypadków – zaokrąglijmy tę wartość do 20%, aby ułatwić nieco obliczenia. Załóżmy również, że wygramy pulę za każdym razem, gdy trafimy flusha (w rzeczywistości trzymalibyśmy najlepszą rękę w około 96% przypadków).
Obliczmy teraz – korzystając z podanego wcześniej wzoru – jak dużo pieniędzy musimy wygrać po trafieniu upragnionego układu, aby nasz call był przynajmniej „break even”:
50 / (50 + 50 + 67 + X) = 0,2
50 / (167 + X) = 0,2
0,2 * 167 + 0,2 * X = 50
33,4 + 0,2 * X = 50
0,2 * X = 16,6
X = 16,6 / 0,2
X = 83$
Trafiając drawa, musimy wygrać od buttona 83$. Pula na riverze będzie wynosiła 167$, co oznacza, że bet rywala na ostatniej ulicy powinien wynosić przynajmniej połowę puli. A pamiętajmy, że buttonowi pozostało jedynie 117$.
Jako że button nie będzie atakować na riverze w 100% przypadków, szczególnie, gdy spadnie karta kompletująca kolor, musiałbyś zrobić jedną z poniższych dwóch rzeczy, aby wyciągnąć potrzebne value:
Zagrać donk-beta
Jeśli wybierzemy tę opcję, odpowiedź naszego przeciwnika musi przynieść nam przeciętnie 83$ zarobku. Przykładowo, jeśli zagralibyśmy donk-bet all-ina za 117$, button musiałby sprawdzić w co najmniej 70% przypadków.
Zagrać check-calla (lub check-raisa)
To zagranie również musi przynieść nam przeciętnie 83$. Przykładowo, rywal musiałby zagrywać all-ina za 117$ w minimum 70% przypadków, aby nasz call na turnie był opłacalny.
Te scenariusze są, owszem, możliwe, ale mało prawdopodobne. W przeciwieństwie do przykładu z KQ, w przypadku trafienia koloru nie będziemy mieli nutsów. Poza tym gramy bez pozycji, a stack efektywny po sprawdzeniu na turnie nie jest wystarczająco wysoki. Wszystko to powoduje, że wyciągnięcie potrzebnej wartości na riverze staje się dużo trudniejsze. Dlatego nie możemy dochodowo sprawdzić na turnie z tak słabą ręką, nawet biorąc pod uwagę implied oddsy.

Button vs big blind (pula z jednym raisem, gramy jako preflop agresor)
Implied oddsów używamy nie tylko wtedy, kiedy posiadamy drawa i mierzymy się z betem. Są one istotne również w tych sytuacjach, kiedy to my betujemy. Zastanówcie się nad następującym spotem:
Raisujesz jako pierwszy z buttona, a big blind sprawdza. Na flopie spadają J85.
Budując swoją strategię c-betów, możesz wziąć pod uwagę implied oddsy. Aby to zademonstrować, weźmy dwie możliwe ręce: J9 i AJ.
Zacznijmy od J9. To ręka, z którą spokojnie możemy value betować na dwóch ulicach, pytanie brzmi więc, jak wyciągnąć największą wartość: powinniśmy betować na flopie i turnie, a potem czekać na riverze? Betować na flopie, czekać na turnie i betować ponownie na riverze? A może czekać na flopie, a potem betować na turnie i riverze?
Przeanalizujmy możliwe scenariusze, kiedy na turnie 9 poprawiamy siłę naszego układu do dwóch par – to dla naszej ręki kluczowa karta:
Scenariusz 1
C-betujesz i zostajesz sprawdzony. Na turnie spada 9. Twój postrzegany zakres jest teraz silniejszy, ponieważ QT, T7s i 76s trafiają swoje drawy. Oznacza to, że wyciągniesz mniej value od swoich dwóch par i narażasz się na tzw. reverse implied oddsy, kiedy twój przeciwnik trzyma QT.
Scenariusz 2
C-betujesz, a rywal przebija. Sprawdzasz, a na turnie spada 9. Twój przeciwnik będzie często barrelować na tym turnie, ponieważ jego zakres znacząco przybrał na sile. Musisz sprawdzić, ale gra na ostatniej z ulic może nie należeć do najłatwiejszych i najprzyjemniejszych.
Scenariusz 3
Czekasz, a na turnie spada 9. Przeciwnik ma teraz mnóstwo potencjalnych blefów w rodzaju AT, KT, T6s, T4s, T3s, T2s, KQ, Q7s, Q6s, Q4s, Q3s, Q2s itd. Będzie wywierać na ciebie dużą presją – wszak QT, T7s i 76 skompletowały swoje układy – ale ty możesz sprawdzać, ponieważ trzymasz bardzo mocną rękę.
Łatwo wyciągnąć wniosek, że najlepszym zagraniem jest check na flopie. Twoja ręka gra bardzo dobrze na turnie z kartą, która poprawia twój układ, a jednocześnie jest dobrym kandydatem do blefów dla rywala.

Teraz zajmijmy się AJ. Z tą ręką na niektórych runoutach możemy dostać nawet trzy ulice wartości, na innych – tylko dwie. Powiedzmy więc, że ręka ta posiada 2,5 ulicy wartości. Jak wyciągnąć najwięcej value?
Ponownie skupmy się na turnie, który daje nam dwie pary – w tym przypadku będzie to as.
Scenariusz 1
C-betujesz, a rywal sprawdza. Turn to as. Karta ta wzmacnia twój zakres, natomiast już niekoniecznie zakres przeciwnika. Dlatego może się wzbraniać przed sprawdzaniem dwóch barreli z rękoma w rodzaju 8x i 5x. Niezależnie od tego, posiadasz bardzo mocny układ, board nie kompletuje żadnego drawa, dlatego niemal zawsze będziesz mógł zagrać trzy bety dla wartości.
Scenariusz 2
C-betujesz, a rywal raisuje. Sprawdzasz, a turn przynosi 9. Karta ta poprawia twój zakres bardziej niż zakres przeciwnika, dlatego będzie on ostrożniejszy w blefowaniu (przynajmniej w teorii). Tak czy inaczej – twoja ręka pokonuje teraz część value range’u przeciwnika, a board nie skompletował żadnych drawów, więc masz łatwego calla.
Scenariusz 3
Zagrywasz check backa, a na turnie spada as. Ta karta znacząco wzmacnia twój zakres, a przeciwnik będzie czekał z bardzo dużą częstotliwością. W rezultacie otrzymasz ograniczoną wartość od jego blefów.
Łatwo można zauważyć, dlaczego c-betowanie z AJ jest w tym spocie koniecznością. Wszystkie scenariusze zachęcają do natychmiastowo budowania puli.

Podsumowanie
Implied oddsy odgrywają dużą rolę nie tylko w sytuacjach, kiedy mierzymy się z betami przeciwników; mają znaczenie również wówczas, gdy sami betujemy. Pomagają w budowie tak zakresów obronnych, jak i zakresów atakujących. Jeśli umiejętnie będziesz z nich korzystać, mogą mieć bardzo pozytywny wpływ na twój win-rate. Właściwie zrozumienie implied oddsów pomoże w częstszym generowaniu bardzo łatwych i dochodowych sytuacji.






